halfmoon

R-CMD-check Codecov test coverage Lifecycle: experimental

Within light there is darkness, but do not try to understand that darkness. Within darkness there is light, but do not look for that light. Light and darkness are a pair like the foot before and the foot behind in walking.

– From the Zen teaching poem Sandokai.

The goal of halfmoon is to cultivate balance in propensity score models.

Installation

You can install the most recent version of halfmoon from CRAN with:

install.packages("halfmoon")

You can also install the development version of halfmoon from GitHub with:

# install.packages("devtools")
devtools::install_github("malcolmbarrett/halfmoon")

Example: Weighting

halfmoon includes several techniques for assessing the balance created by propensity score weights.

library(halfmoon)
library(ggplot2)

# weighted mirrored histograms
ggplot(nhefs_weights, aes(.fitted)) +
  geom_mirror_histogram(
    aes(group = qsmk),
    bins = 50
  ) +
  geom_mirror_histogram(
    aes(fill = qsmk, weight = w_ate),
    bins = 50,
    alpha = 0.5
  ) + scale_y_continuous(labels = abs)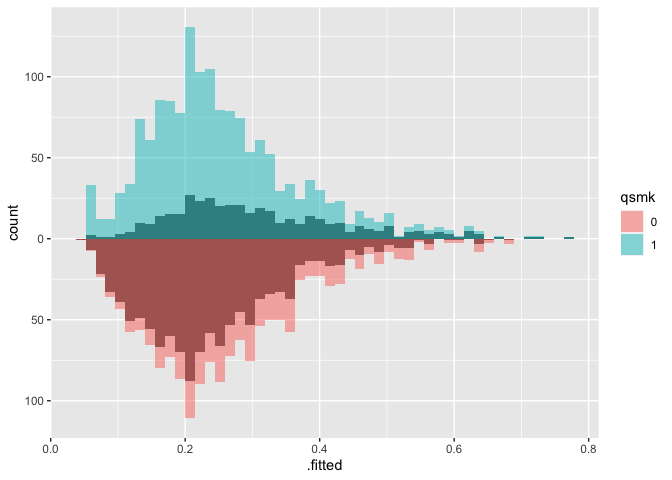


# weighted ecdf
ggplot(
  nhefs_weights,
  aes(x = smokeyrs, color = qsmk)
) +
  geom_ecdf(aes(weights = w_ato)) +
  xlab("Smoking Years") +
  ylab("Proportion <= x")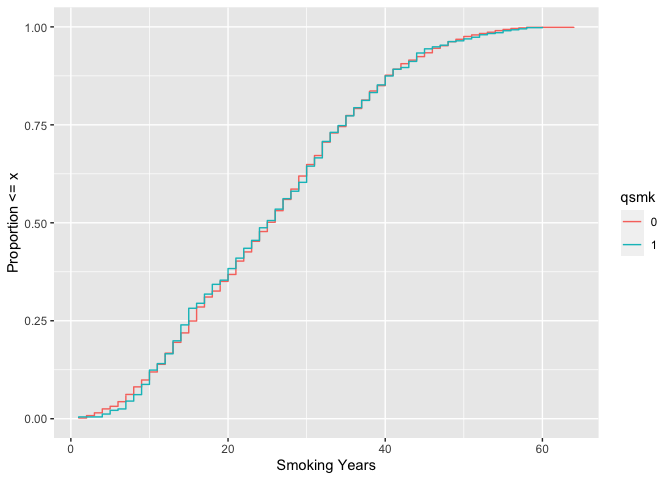


# weighted SMDs
plot_df <- tidy_smd(
  nhefs_weights,
  race:active,
  .group = qsmk,
  .wts = starts_with("w_")
)

ggplot(
  plot_df,
  aes(
    x = abs(smd),
    y = variable,
    group = method,
    color = method
  )
) +
  geom_love()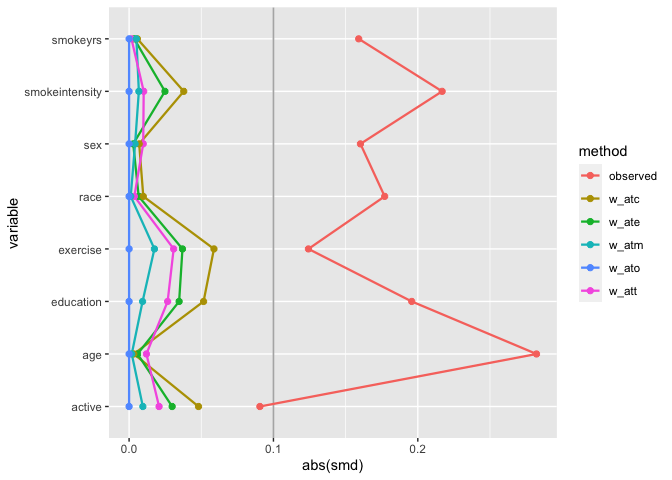

Example: Matching

halfmoon also has support for working with matched datasets. Consider these two objects from the MatchIt documentation:

library(MatchIt)
# Default: 1:1 NN PS matching w/o replacement
m.out1 <- matchit(treat ~ age + educ + race + nodegree +
                   married + re74 + re75, data = lalonde)

# 1:1 NN Mahalanobis distance matching w/ replacement and
# exact matching on married and race
m.out2 <- matchit(treat ~ age + educ + race + nodegree +
                   married + re74 + re75, data = lalonde,
                   distance = "mahalanobis", replace = TRUE,
                  exact = ~ married + race)

One option is to just look at the matched dataset with halfmoon:

matched_data <- get_matches(m.out1)

match_smd <- tidy_smd(
  matched_data,
  c(age, educ, race, nodegree, married, re74, re75), 
  .group = treat
)

love_plot(match_smd)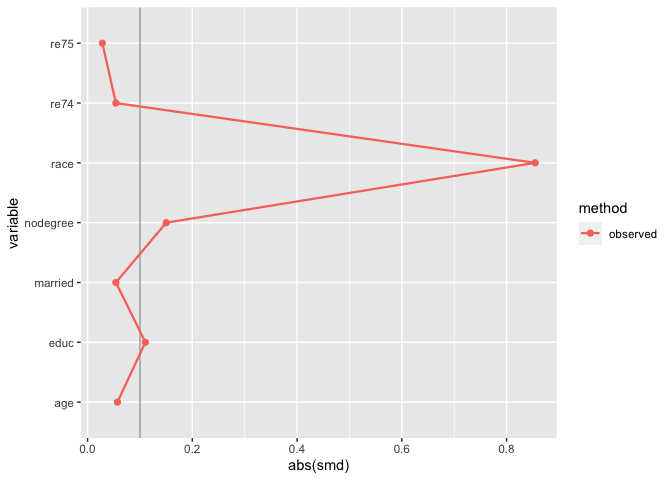

The downside here is that you can’t compare multiple matching strategies to the observed dataset; the label on the plot is also wrong. halfmoon comes with a helper function, bind_matches(), that creates a dataset more appropriate for this task:

matches <- bind_matches(lalonde, m.out1, m.out2)
head(matches)
#>      treat age educ   race married nodegree re74 re75       re78 m.out1 m.out2
#> NSW1     1  37   11  black       1        1    0    0  9930.0460      1      1
#> NSW2     1  22    9 hispan       0        1    0    0  3595.8940      1      1
#> NSW3     1  30   12  black       0        0    0    0 24909.4500      1      1
#> NSW4     1  27   11  black       0        1    0    0  7506.1460      1      1
#> NSW5     1  33    8  black       0        1    0    0   289.7899      1      1
#> NSW6     1  22    9  black       0        1    0    0  4056.4940      1      1

matches includes an binary variable for each matchit object which indicates if the row was included in the match or not. Since downweighting to 0 is equivalent to filtering the datasets to the matches, we can more easily compare multiple matched datasets with .wts:

many_matched_smds <- tidy_smd(
  matches,
  c(age, educ, race, nodegree, married, re74, re75), 
  .group = treat, 
  .wts = c(m.out1, m.out2)
) 

love_plot(many_matched_smds)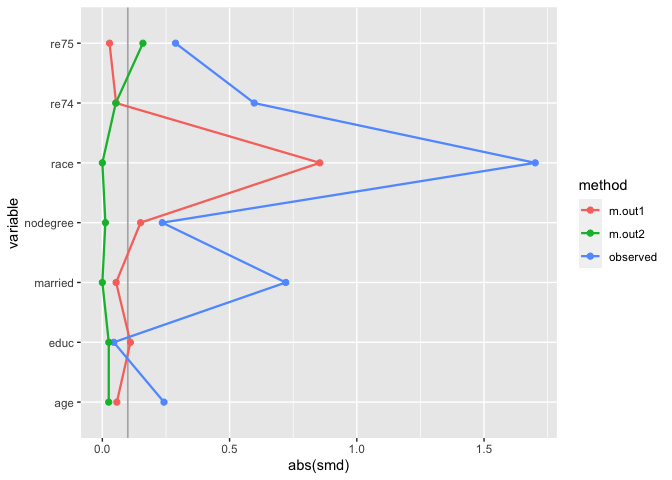

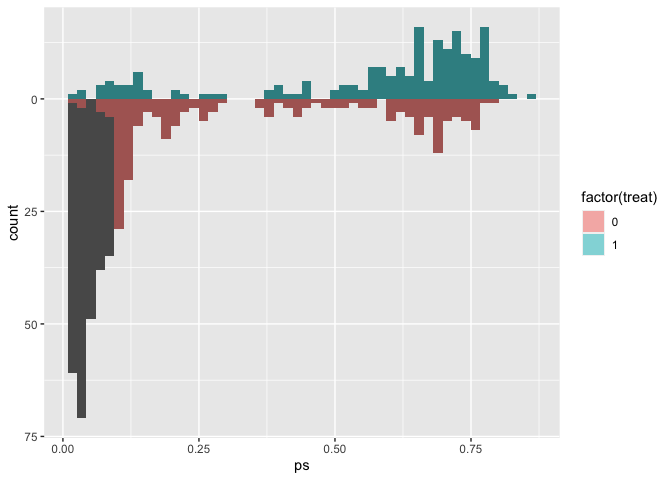
We can also extend the idea that matching indicators are weights to weighted mirrored histograms, giving us a good idea of the range of propensity scores that are being removed from the dataset.

# use the distance as the propensity score
matches$ps <- m.out1$distance

ggplot(matches, aes(ps)) +
    geom_mirror_histogram(
        aes(group = factor(treat)),
        bins = 50
    ) +
    geom_mirror_histogram(
        aes(fill = factor(treat), weight = m.out1),
        bins = 50,
        alpha = 0.5
    ) + scale_y_continuous(labels = abs)